# code for loading notebook's format
import os
# path : store the current path to convert back to it later
path = os.getcwd()
os.chdir(os.path.join('..', '..', '..', 'notebook_format'))
from formats import load_style
load_style(css_style='custom2.css', plot_style=False)
os.chdir(path)
%load_ext watermark
%load_ext autoreload
%autoreload 2
import torch
import numpy as np
import pandas as pd
import transformers
import torch.nn.functional as F
from datasets import load_dataset
from transformers import (
AutoTokenizer,
AutoModelForCausalLM,
)
from peft import LoraConfig
from trl import DPOTrainer, DPOConfig
%watermark -a 'Ethen' -d -v -u -p transformers,datasets,torch,trl,peft
Direct Preference Optimization (DPO)¶
A typical process of training modern LLM involves an un/self-supervised training stage, followed by an instruction tuning stage. The instruction tuning phase trains LLM on higher quality of instructions to completion datasets. This helps conform the model's outputs with desired behaviors or tasks, making it more reliable and effective for various applications. Despite the success of instruction tuning, relative judgements of response quality are often times easier to collect, thus subsequent LLM works have a so called alignment stage, which tunes LLMs with preference dataset and reinforcement learning based algorithms, a.k.a. RLHF (Reinforcement Learning with Human Feedback).
In Reinforcement Learning from Human Feedback (RLHF), our objective can be written as:
$$ \max_{\pi_{\theta}} \mathbb{E}{x \sim D, y \sim \pi_{\theta}(y|x)}[r(x, y)] - \beta \cdot \mathrm{KL}(\pi_{\theta}(y|x)||\pi_{\mathrm{ref}}(y|x)) $$- This objective function optimizes our LLM policy $\pi_{\theta}$ to maximize the expected reward $[r(x, y)]$ for the questions/prompts $x$ sampled from our dataset $D$ and the answers $y$ generated by LLM policy $\pi_{\theta}(y|x)$. The reason we can't just run gradient descent on this objective function and resort to RL algorithms is because the output $y$ are sampled from LLM using various decoding strategies (greedy, beam search, etc.). All of which are not differentiable.
- At the same time, it seeks to minimize Kullback-Leibler (KL) divergence between the LLM policy $\pi_{\theta}(y|x)$ and the original reference policy $\pi_{\mathrm{ref}}(y|x)$, weighted by a factor $\beta$. Higher $\beta$ means less deviation from the reference model. This second term is added to prevent "reward hacking," a situation where the LLM generates sequences of tokens that achieve high reward scores but may be nonsensical.
Given this objective function, RLHF methods usually involves fitting a reward model to dataset of human preferences and then use RL to optimize a language model policy to produce responses assigned high reward without drifting excessively far from the original model.
Suppose we have a preference dataset at hand, we can convert these preferences into a score by modeling it via the Bradley-Terry model.
$$\Pr(y_1 \succ y_2) = \frac{\exp(r(x, y_1))}{\exp(r(x, y_1)) + \exp(r(x, y_2))}$$where:
- $P(i \succ j)$ represents probability that the first answer ($y_1$) is better than the second answer ($y_2$) in a paired comparison.
- The numerator $\exp(r(x, y_1))$ is the (hidden) reward function that evaluates the first answer's quaility $y_1$ for an input prompt $x$. Similarly, for the second answer, we have $\exp(r(x, y_2))$.
- The probability is computed by taking the ratio of first answer's reward over the sum of rewards for both answers. This normalization ensures we result in a valid probability distribution.
We can parameterize the reward function and estimate its parameter via maximum likelihood, which boils down to framing it as a binary classfication problem:
$$ L = -\mathbb{E}_{(x,y_1,y_2)\sim D}\left[\log \sigma\left(r(x,y_1) - r(x,y_2)\right)\right] $$Where $\sigma$ is the logistic function $\frac{1}{1 + e^{-x}}$.
Note, we can show the two are connected. Assuming $r(x,y_1) = A$ and $r(x,y_2) = B$
$$ \frac{e^A}{e^A + e^B} = \frac{\frac{e^A}{e^A}}{\frac{e^A + e^B}{e^A}} = \frac{1}{1 + \left(\frac{e^A + e^B}{e^A} - 1\right)} = \frac{1}{1 + \left(\frac{e^A + e^B - e^A}{e^A}\right)} = \frac{1}{1 + \left(\frac{e^B}{e^A}\right)} = \frac{1}{1 + e^{B-A}} = \sigma(A - B) $$While RLHF is capable of producing models with impressive capabilities (supposedly one of the secret sauces behind ChatGPT), its pipeline can be consideraby more complex than supervised learning. Involving training multiple LMs and sampling from a LLM policy as part of the training loop. One of the key insights in Direct Preference Optimization (DPO) [9] is replacing this complex process in RLHF with a supervised learning algorithm that implicitly optimizes the same objective as RLHF.
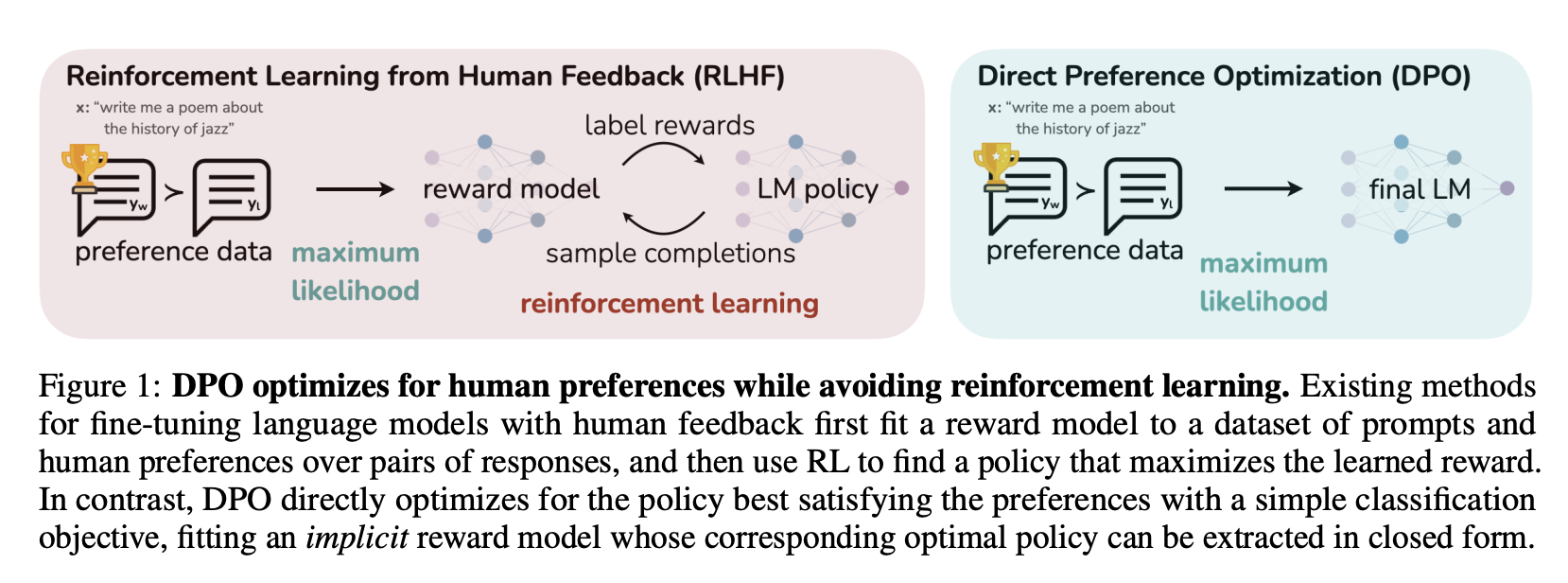
The DPO paper shows an optimal solution to this optimization problem is:
$$\pi_{\theta}(y|x) = \frac{1}{Z(x)} \pi_{\mathrm{ref}}(y|x) \exp\left(\frac{1}{\beta}r(x, y)\right)$$where:
$$Z(x) = \sum_{y'} \pi_{\mathrm{ref}}(y'|x) \exp\left(\frac{1}{\beta}r(x, y')\right)$$While an exact solution exists, it is hard to utilize in practice. $Z(x)$ entails we would have to compute all possible answers that can be generated by our LLM, making it computationally intractable.
The trick is to re-arrange the above term to be based on the reward function:
$$\log \pi_{\theta}(y|x) = \log \left[\frac{1}{Z(x)}\pi_\text{ref}(y|x) \exp \left(\frac{1}{\beta} r(x,y)\right)\right] = \log \pi_\text{ref}(y|x) - \log Z(x) + \log \exp \left(\frac{1}{\beta} r(x,y)\right) = \log \pi_\text{ref}(y|x) - \log Z(x) + \frac{1}{\beta} r(x,y)$$$$r(x, y) = \beta \log \frac{\pi_{\theta}(y|x)}{\pi_{ref}(y|x)} + \beta \log Z(x)$$Given this reward function expression, we can now plug it back into Bradley-Terry model expression:
$$P(y_1 > y_2) = \sigma(r(x, y_1) - r(x, y_2)) = \sigma \left( \beta \log \frac{\pi_{\theta}(y_1|x)}{\pi_{ref}(y_1|x)} + \beta \log Z(x) - \beta \log \frac{\pi_{\theta}(y_2|x)}{\pi_{ref}(y_2|x)} - \beta \log Z(x) \right)$$With the Bradley-Terry model depending only on reward differences beteen the two completions, the computationally expensive $Z(x)$ term canels out. With the final DPO loss being:
$$L_{DPO}(\pi_{\theta}; \pi_{ref}) = -\mathbb{E}{(x,y_1,y_2)\sim D} \left[ \log \sigma \left( \beta \log \frac{\pi_{\theta}(y_1|x)}{\pi_{ref}(y_1|x)} - \beta \log \frac{\pi_{\theta}(y_2|x)}{\pi_{ref}(y_2|x)} \right) \right]$$And with all that, we now have the probability of human preference data in terms of our optimal policy rather than a reward model.
Similar to existing algorithms, Direct Preference Optimization (DPO) uses a preference model, such as the Bradley-Terry model, to evaluate how well a reward function aligns with empirical preference data. However, while RLHF methods trains a reward model based on the preference model and then optimize a policy to maximize that learned reward, DPO takes a different approach. It uses a change of variables to directly define a preference loss as a function of the policy itself. This is DPO's main contribution - an algorithm that can train language models from human preferences through binary cross-entropy objective, discarding the need for reinforcement learning methods.
Implementation¶
This implementation section is comprised of two parts. We'll roll out the DPO loss calculations ourselves, as well as showcase how to leverage trl library's DPOTrainer [3] [5]. We'll be leveraging Ultrafeedback [10] as our dataset. Ultrafeedback is a synthetic preference dataset collected via LLMs. At a high level, the authors compiled 60K diverse instructions, prompted a pool of distinct models at different capability levels for generating completions, and finally leveraged GPT-4 for annotating completion pairs.
dataset = load_dataset(
"argilla/ultrafeedback-binarized-preferences-cleaned",
split="train",
verification_mode="no_checks",
cache_dir="/data"
)
print(dataset)
dataset[0]
def create_preference_triplets(example):
"""
Create preference triplets:
- `prompt`: prompt that is given to a model for text generation.
- `chosen`: preferred generated response for the corresponding prompt.
- `rejected`: response that is not preferred.
"""
chosen = extract_assistant_messages(example["chosen"], index=-1)
rejected = extract_assistant_messages(example["rejected"], index=-1)
return {
"prompt": example["prompt"],
"chosen": chosen,
"rejected": rejected
}
def extract_assistant_messages(messages, index=-1):
"""Recursively extract the last assistant messages from the end of the conversation."""
if messages[index]["role"] == "assistant":
return messages[index]["content"]
else:
extract_assistant_messages(messages, index - 1)
dataset_dict = dataset.train_test_split(test_size=0.01, seed=54321)
dataset_dict_preprocessed = dataset_dict.map(
create_preference_triplets,
num_proc=8
)
dataset_dict_preprocessed["train"][0]
For DPO, we need two copies of the model, one serving as the model/policy we wish to optimize, and another for reference model, hence memory requirement will be higher than supervised fine-tuning.
model_name_or_path = "Qwen/Qwen2.5-0.5B-Instruct"
tokenizer = AutoTokenizer.from_pretrained(model_name_or_path, cache_dir="/data")
tokenizer.padding_side = "left"
tokenizer.pad_token = tokenizer.eos_token
reference_model = AutoModelForCausalLM.from_pretrained(
model_name_or_path,
cache_dir="/data"
)
reference_model.eval()
model = AutoModelForCausalLM.from_pretrained(
model_name_or_path,
cache_dir="/data"
)
model.train()
def get_batch_logps(logits, labels, label_pad_token_id = -100):
"""
Get log probabilities summed over all tokens for a given batch.
Parameters
----------
logits: [batch size, seq length, vocab size]
labels: [batch size, seq length]
Returns
-------
logps: [batch size]
"""
# next token prediction: labels are inputs shifted by one
targets = labels[:, 1:].clone()
# truncate logits to match labels' number of tokens
logits = logits[:, :-1, :]
loss_mask = targets != label_pad_token_id
# dummy token; we'll ignore loss on these tokens later
targets[targets == label_pad_token_id] = 0
log_probs = logits.log_softmax(dim=-1)
# [batch size, seq length]
per_token_logps = torch.gather(log_probs, dim=2, index=targets.unsqueeze(2)).squeeze(2)
return (per_token_logps * loss_mask).sum(-1)
example = dataset_dict_preprocessed["train"][0]
prompt = example["prompt"]
chosen = example["chosen"]
rejected = example["rejected"]
chosen_tokenized_outputs = tokenizer([prompt + chosen], padding=True, return_tensors="pt")
policy_chosen_model_outputs = model(
chosen_tokenized_outputs["input_ids"],
chosen_tokenized_outputs["attention_mask"]
)
policy_chosen_logps = get_batch_logps(
policy_chosen_model_outputs.logits,
chosen_tokenized_outputs["input_ids"]
)
rejected_tokenized_outputs = tokenizer([prompt + rejected], padding=True, return_tensors="pt")
policy_rejected_model_outputs = model(
rejected_tokenized_outputs["input_ids"],
rejected_tokenized_outputs["attention_mask"]
)
policy_rejected_logps = get_batch_logps(
policy_rejected_model_outputs.logits,
rejected_tokenized_outputs["input_ids"]
)
with torch.no_grad():
reference_chosen_model_outputs = reference_model(
chosen_tokenized_outputs["input_ids"],
chosen_tokenized_outputs["attention_mask"]
)
reference_chosen_logps = get_batch_logps(
reference_chosen_model_outputs.logits,
chosen_tokenized_outputs["input_ids"]
)
reference_rejected_model_outputs = reference_model(
rejected_tokenized_outputs["input_ids"],
rejected_tokenized_outputs["attention_mask"]
)
reference_rejected_logps = get_batch_logps(
reference_rejected_model_outputs.logits,
rejected_tokenized_outputs["input_ids"]
)
def dpo_loss(
policy_chosen_logps,
policy_rejected_logps,
reference_chosen_logps,
reference_rejected_logps,
beta=0.1,
):
"""logps shape [batch size,]"""
chosen_logratios = policy_chosen_logps - reference_chosen_logps
rejected_logratios = policy_rejected_logps - reference_rejected_logps
logits = chosen_logratios - rejected_logratios
loss = -F.logsigmoid(beta * logits).mean(dim=-1)
return loss
dpo_loss(
policy_chosen_logps,
policy_rejected_logps,
reference_chosen_logps,
reference_rejected_logps,
)
DPOTrainer¶
training_args = DPOConfig(
output_dir="./dpo_sample_model",
fp16=True,
gradient_accumulation_steps=4,
per_device_train_batch_size=1,
per_device_eval_batch_size=2,
gradient_checkpointing=True,
gradient_checkpointing_kwargs={"use_reentrant": False},
max_steps=100,
logging_steps=50,
learning_rate=0.0001,
beta=0.1,
max_length=512,
max_prompt_length=256,
remove_unused_columns=False,
eval_strategy="steps",
eval_steps=50,
save_strategy="steps",
save_steps=50,
)
peft_config = LoraConfig(
r=16,
target_modules=[
"q_proj",
"k_proj",
"v_proj",
"o_proj",
"down_proj",
"up_proj",
"gate_proj"
],
modules_to_save=[
"embed_tokens",
"lm_head"
]
)
dpo_trainer = DPOTrainer(
model,
train_dataset=dataset_dict_preprocessed["train"],
eval_dataset=dataset_dict_preprocessed["test"],
tokenizer=tokenizer,
args=training_args,
peft_config=peft_config,
)
dpo_trainer.train()
DPO trainer offers several metrics related to rewards for us to monitor as part of its training process:
- rewards/chosen: for the chosen responses, it measures the mean difference between policy model and reference model's log probabilities, scaled by beta
- rewards/rejected: Same as above but for rejected responses.
- rewards/accuracies: how often rewards/chosen is greater than its corresponding rewards/rejected.
- rewards/margins: the mean difference between the chosen and corresponding rejected rewards.
We can also compare final result using LLM as a parwise judge. In our case, this boils down to comparing the answer generated by the original base/instruct model with the model that was aligned using DPO.
llm_judge_responses.parquet shows pairwise comparison of a Qwen 2.5 3B instruct reference model versus the reference model being aligned with DPO on ultra feedback dataset.
- 3B model was trained via
dpo_train.py(took approx. 1 hour on 16 A100) - response generated via
generate.py - LLM based judgements curated via
claude_judge.py. LLM as a judge script is largely following the concept introduced as part of a separate notebook, except we call claude through AWS bedrock's API for obtaining judge response.
df_llm_judge_responses = pd.read_parquet("llm_judge_responses_v7.parquet")
print(df_llm_judge_responses.shape)
df_llm_judge_responses.head()
# dpo model preferred 42%
# instruct model preferred 23%
index = 0
print(df_llm_judge_responses["prompts"].iloc[index])
print("\n instruct model response: \n")
print(df_llm_judge_responses["responses1"].iloc[index])
print("\n dpo model response: \n")
print(df_llm_judge_responses["responses2"].iloc[index])
Since DPO was introduced, subsequent works such as IPO, KPO have attempted to further improve upon it. Though, thorough comparisons on these approaches thus far seems to indicate that they all offer similar performance when hyperparameters scans are properly conducted [4].
Reference¶
- [1] Youtube: Direct Preference Optimization (DPO) explained
- [2] Youtube: CS 285: Eric Mitchell: Reinforcement Learning from Human Feedback: Algorithms & Applications
- [3] Huggingface Blog: Fine-tune Llama 2 with DPO
- [4] Huggingface Blog: Preference Tuning LLMs with Direct Preference Optimization Methods
- [5] RLHF in 2024 with DPO & Hugging Face
- [6] Unveiling the Hidden Reward System in Language Models: A Dive into DPO
- [7] Github: DPO - Direct Preference Optimization
- [8] Deriving DPO’s Loss
- [9] Rafael Rafailov, Archit Sharma, Eric Mitchell et al. - Direct Preference Optimization: Your Language Model is Secretly a Reward Model (2023)
- [10] Ganqu Cui, Lifan Yuan, et al. - UltraFeedback: Boosting Language Models with Scaled AI Feedback (2023)